menu
記事作成日：2019年２月19日
記事更新日：2020年３月16日
知識を創生する人間同士の対話（2018.07.28 第６回研究拠点創成フォーラム）
「数学とは何か？」ときかれると、どのようなイメージをもつだろうか。学校で習う方程式や関数などの数式や記号を用いた代数学、もしくは三平方の定理など図形がみえる幾何学などが頭に浮かぶ人が多いだろう。一般的に、数学には「数字や記号を用いて、ノートや黒板に表現され、それをもとに議論をする」という特徴がある。それ故、数学の授業も、教科書に示された記号を用いて例題を解く、練習問題を解く、章末問題を解く…このような風景が未だ多いのではないか。しかしながら、こう考え直すことはできないだろうか。「数学とは既にそこにあるものではなく、継続中の人間活動そのものであり、さらに活動によって生まれるものであり、それ故学ばれる数学とは、未だそこにない何かである」と。
本クラスタのリーダー：影山和也先生（以下、敬称略）は、博士課程の研究から継続的に数学の認識論と図形について興味を持ち続けてきた。現在、基盤研究（B）「教室での知識の創出と進化を促す学習作業空間の構成に関する総合的研究」（平成29年度~33年度）を得て、図形の教育を事例としながら、数学教育やその学習空間について研究を深めている。「いまの数学の教科書はあらかじめストーリーが決められている」と断言する影山。今回は、これまでの経緯、数学のことをどのように考えているのか、どんな教育を理想と考えているのか、どんな研究が必要と考えているのか、ストレートに教えていただいた。
「知識創生」研究クラスタリーダーの影山和也先生
「広島大学は認識論をキチッとやる伝統がある。」と言う影山。認識論とはすなわち、「数学とは何か？」「知識とは何か？」など根本から考えることである。例えば「知識を英語で言うと？」と尋ねられれば、多くが「Knowledge」と答える。しかし、それは知識の一側面にすぎない。影山は「Knowing」と「Knowledge」の２種類があると説明する。
「Knowing」は「知り方」である。すなわち、「学習者は自らの経験を参照したり、知っているものになぞらえて認識する」という生徒自身の知り方である。生徒という主体・行為者が自分自身で新しい知識や視点を生み出す。そこには、生徒のパーソナルでプライベートな世界が存在する。その知識が他者とともに公共化された、すなわちパブリックになって集積されたものが「Knowledge」である。その知識の公共性がいったん担保されるのが教室空間であり、その先には世界全体がある。数学の教科書に示された公式は世界全体で公共化された「Knowledge」であると言えよう。世界の人々は各教室で何が議論され、そこでの当事者らが何を我が物としたかは知り得ないが（knowing）、世界中の誰もが「三平方の定理」を知っている（knowledge）。
■これまでの“文化・社会中心”の教科教育はKnowledgeを学んでいる
さて、数学教育とは、Knowledgeを学ぶことなのか、Knowingを学ぶことなのだろうか。影山はこのフレームワークをもとに、基本的には後者の立場をとると示した上で、これまでの数学教育はKnowledgeを学んできたと説明する。
「数学はなぜ学ぶ必要があるのか？」誰もが一度は頭に浮かぶ疑問だろう。教育的な意義が多くあることは気づくが、なぜ必要かと言われれば「社会・学校教育の要請があるから」である。影山は「今は産業社会だから必要なのであって、もし社会が変化したら、少なくとも教科書にある数式は不要になる」と言い切る。教科書に「解の公式」が説明されているから学ぶ必要があるのであり、進路を保証のために学ぶ必要がある。このように社会的に必要とされているからやる教育を“文化・社会中心”の教科教育と影山は呼ぶ。そこに行為者はおらず、社会の中で公共化された「Knowledge」がただそこに存在するのだ。
■これからは“人間中心”のKnowingする数学学習を！
「学習指導要領にあるからやる、というのは制度からみた学ぶ意義。しかし知識はあらかじめ存在するものではない。人間がつくりだすものだ。」このような認識論・学習論にたち、数学教育を見直していこうとしている。そのためには、学習者である生徒中心の数学教育を考え、現在進行系のKnowingに着目する。
「ニエーブンノマイナスビープラスマイナスルート…という解の公式をつかって数式を解くことに何の意味もない。それよりも、なぜ人間はそれを解くのか？なぜ人間は公式をつくるのか？人間はどのように考えそれをつくっていくのか？そんなことを考えたい。“人間中心”の教科教育をしたい」
このように影山は“学習者中心”という表現ではなく“人間中心”という表現をつかう。その理由には、影山の「現成主義」(enactivism)という認知論・認識論の立場にある。現成主義とは、生物としての人間の振る舞いに関心をもち、世界も心も行為・運動から産出されるという考え方である。構成主義も、知識を作るのは人間であり、相互作用の対象である環境が前提として、現状主義は、まず生物としての人間があり、自らの行為によって、行為自体ができるような世界を作り出していくとする。したがって、人間の生物的な特徴・身体的な特徴もふくめて議論することが可能だ。影山が現成主義の考えを取り入れたのは、平成29年の身体化デザイン研究フォーラムへ参加した際のDr.Abrahamsonとの出会いが大きい。
現在日本の教育改革の中で学力観が変化し、資質・能力ベースへ動こうとしている。これに合わせて教科書も変化する必要があり、学校現場で行われる数学の授業も変化する必要があるし、さらにその子どもの学習を捉える教育学としての研究方法も変化する必要がある。そこへの示唆に向けて今回の科研の大きな２つの目的がある。新しい研究方法論を導く「①理論・哲学研究」をすること、そしてそれを学校現場で実践するために「②探索的・開発的研究」をすること。
現成主義についての説明
（平成30年数学教育心理国際学会での発表資料より引用。資料はコチラ。）
先述した通り、数学では「記号をもとに議論をする」という特徴がある。数学的世界にある目に見えないものを、数学的記号を用いて目に見えるカタチにして、ノートや黒板上で表現してはじめて、他者と議論・コミュニケーションができる。その状況を現成主義で捉える際の鍵概念が「有意味世界の生成（bringing forth a world of significance）」である。日本数学教育学会第50回秋期研究大会「有意味世界の生起としての数学学習―数学の学習と指導への現場主義的アプローチ―」という題目で、発表し、以下のように説明している。
構成主義は、自分自身の経験しうる境界を超えるような世界にある事柄が真であるかどうかを確かめる術を持たない。（中略）構成主義においては、知ることは妥当な適応（fit）であり、この点は現成主義とも一貫するが、行為者を区分可能な環境の一部と見なす現成主義においては、（中略）行為者にとってどのような意味を持つか、何が重要であるか、どこまでが認められた振る舞いかを、一つの世界として行為者自身が創出することを主張する。これが有意味世界の生起であり、行為者は自らが環境と相互作用的に生起させる世界のなかで振る舞っている。
影山（2017）pp.466-467
このように空間における環境面を重視する考え方、生物の進化などの考え方で教室をみれば、人、教室のもの、みえるもの、さわるものすべてを含んだ「学習空間」において「知識創成」する。これがユニット名とクラスタ名の由来になっている。
日本数学教育学会第50回秋期研究大会発表資料(クリックするとPDFが開きます。)
■現成主義と「身体性」
「知識をつくる時はリズムがあるんです。人間の身体の中の理解しやすいリズムが。例えば、『にーしーろーやーとぅ』という偶数の列は、とても理解しやすい。」
このように知識を創成する際には、身体との関連性に注目している。それが身体化、もっとこえて有意味世界の生起へなるそのとき、パターンやリズムがある。「例えば、一次関数ｙ＝ｘという直線を学ぶとき、一定変化をわかるとき、それは『イチ、ニィ、サン、シィ、ゴッ・・・』のように数える。このリズムで数えることによって、１も２も３も４も５も同じもの（単位）として自然に認識できる。これが身体化の事例です。」と説明してくれた。筆算、解の公式、多項式の展開など、手順をふめば自動的に答えがでてくるアルゴリズムや、生徒が直感の中で考えやすい図形を扱った数学は、この身体化のよい事例になるという。
影山が図形に注目する理由をきいてみると、「単純に面白いから！もあるけど、考えやすいから」と説明し「数学らしさがでる。博論でspatial reasoning（空間的推論）をテーマにしたというのもあります。」とこたえた。たとえば、日本では中学校２年生で証明の単元があるが、それを学んだ際に違和感をもった人も多いのではないだろうか。それまでの図形を考えていた生徒の世界が、言葉の世界になっていくのだ。このような立場で研究を進めたり海外の研究者との交流を通して、西洋と東洋での学問の捉え方の違いの傾向も感じてきた。西洋は、身体を捨て、客観的なものとして捉える一方、東洋は人・身体(Body)を意識し、その理解に努める。この現成主義や身体化の議論は、全く目新しいものではなく、東洋に位置づく我が国においては、むしろ自然な発想であるとも言える。現代ではもはや洋の東西の違いを問うことはナンセンスなのかもしれないが、人の認識の仕方に「言語を超える」(beyond words)ものがあるという洞察は十分に共感されるのではないだろうか。
【具体的な取組１】 数学研究者と共演するフォーラムの開催
2018年７月28日には、数学者（独立研究者）である森田真生先生をお招きし、知識創成フォーラムを開催した。森田先生は、主著『身体する数学』などで、数学の身体性に注目している研究者である。森田先生の講演後には、影山先生と森田先生の対談があり、数学と身体、being-knowing-doingを一体とする思想、そこでの対話により知を創造する人間の学び本来に改めてふれることができた。開催報告の詳細は、こちら。
|
|
|
集合写真
■数学的学習空間の研究方法論を見出していく
本科研での「身体化」「現成主義」に基づく数学研究を進めるなかで、影山は教室空間・子どもにとっての学習空間の複雑さをするために枠組みとその捉え方に関する「研究方法論」を見出している。そして作業空間・学習空間を分析する際の枠組みをつくりだし、その研究方法論の妥当性を検証している。教室の学習空間においては、「生徒は何に従事し没頭しているか（engagement）」「行為を支える多様な世界は教室のなかでどのように同居するか」「世界の多様さにあいまって行為の変容を促す要因は何か」「実践中の数学的対象の位置や役割は何か」という４つの分析枠組みを見出した。また、その際は「Theoretical knowing」「Actual knowing」「Possible knowing」という子どもの３つの認識様式を枠組みにできないかと考えている。広島大学の付属小と共同研究してきた成果である。
例えば、初等第３学年の三角形の定義の授業において、子どもは正三角形の教材ツールを使用してactualにKnowingする。その後、いろんな三角形と思われる図形をみつけていくpossibleのKnowingに移る。そこから、三角形の定義をみつけだすtheoreticalなKnowingをしつつ、定義からさらに新しい三角形の可能性を探るpossibleなKnowingを繰り返す。さらに、三角形を測量や比較をするactualなKnowingをしながら、定義を見直すtheoreticalなKnowingをするという往還もある。
「このような「Theoretical knowing」「Actual knowing」「Possible knowing」という３つの枠組みは、他領域・他教科でもつかえないか。そうしたら、教科の特性がみえてくる。」と影山。たとえば、数学であれば、actualからすぐにtheoricalに移行する、もしくはtheoricalからactualする、といった特徴があるという。これは他の領域・教科でも同様なのか異なるのか。同様であれば理論化できるし、異なれば数学らしさの特徴を見出すことができる。多くの領域で可能になれば、授業への還元の視点が見込まれる。このようにして、学習空間における知識創成を捉える分析枠組み・研究方法を見出すことが、本科研の大きな目標だ。数学的学習作業空間（mathematical working space theory）の理論化を図っている。本成果は、数学教育心理国際学会第42回研究大会（42th Annual Meeting of the International Group for the Psychology of Mathematics Education）で発表（クリックすると発表スライドが開きます）し、ジャーナルに投稿準備中である。
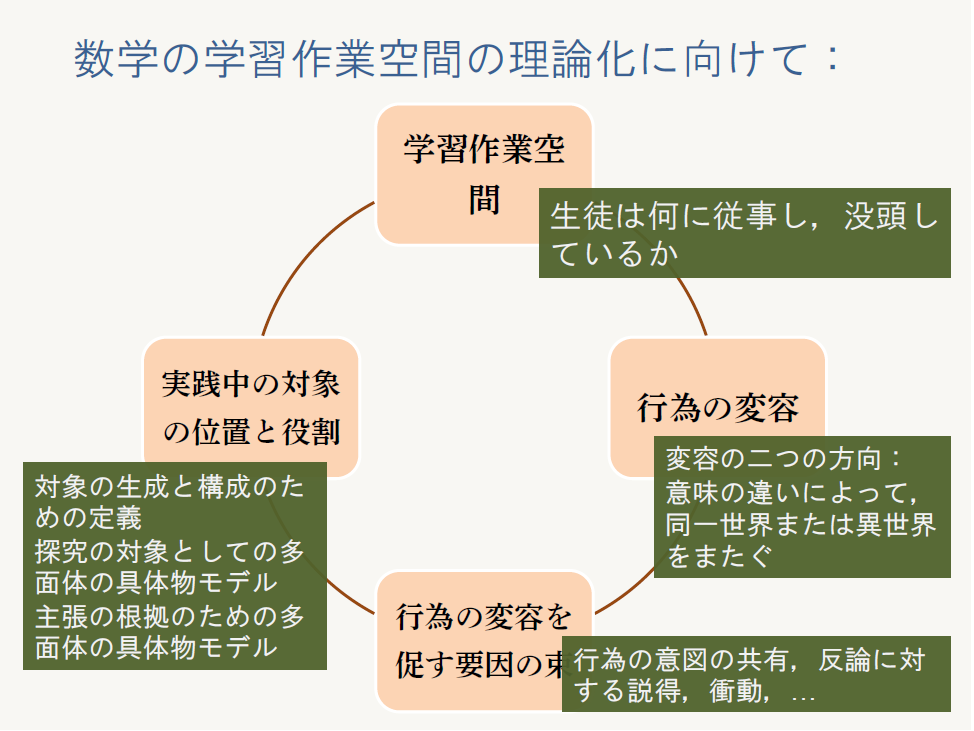
数学の学習作業空間を捉える４つの分析枠組み
（日本数学教育学会第50回秋期研究大会での発表資料より引用。資料はコチラ。）
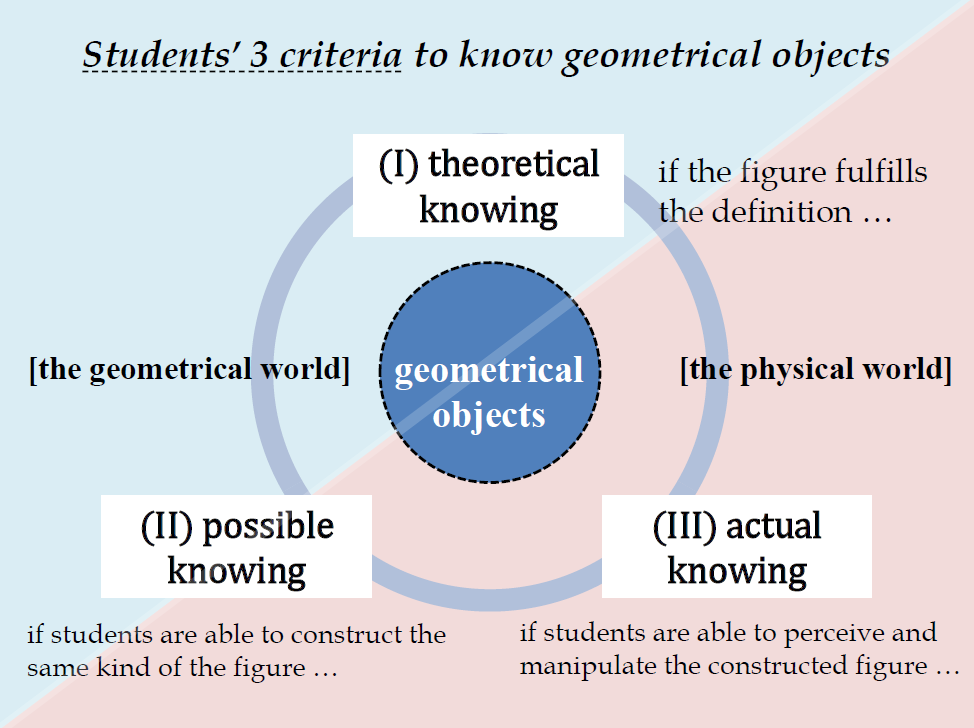生徒による３つの認識様式
（平成30年数学教育心理国際学会第42回研究大会での発表資料より引用。資料はコチラ。）
■他分野の研究者と連携し研究方法・分析方法を広げていく
本科研は、数学教育を専門とする小山正孝先生による数学的理解のプロセス-プロダクトのアイデアを参照しつつ、専門とする教科が異なる多様な研究者で構成され、お互いの得意領域を結集していることも大きな特徴だ。理由は、上記のように他教科で検証したいという理由はあるが、それだけではない。そもそもの研究方法・分析方法を他学問の知見を取り入れ、拡張もしくは洗練させたいと考えている。
今回のクラスタの一員である、日本語教育を専門とする永田良太先生からは談話分析の方法を学んでいる。心理学を専門とする森田愛子先生からは描かれた作品の視覚的な分析方法を学んでいる。また、臨床的なことは特別支援教育が専門の川合紀宗先生、他教科への応用は外国語学習が専門の松宮奈賀子先生が大まかな分担になっている。
「きっかけはEVRIですね。」
これまで同じ研究科の研究者であっても、顔や名前は知っているが、どんな研究をしているのか教科横断的に知る機会は少なかった。EVRIのような他学問の研究者が集まって、それぞれの研究方法や分析を広げていける価値はあるという。今回の科研では、これまで数学を専門とした研究が中心であったが、４～５年目は他教科への波及を考えていく計画だ。「対象物・記号→議論」という数学の特徴が、他の教科にうまく転用できるかは不安であるが、「そもそも論を好む教科には、いいのでは？」と将来を見据えている。
これほど壮大な取り組みを実行している影山だが、「研究方法を理論化するのはいいけど、現場の教師が腑に落ちてくれるものをつくりたい」とも語る。先に定義がある学問書のような書き方の教科書、学習指導要領にあるからやる公式…このような「活動の捨象された、でがらしで面白くない」ものを、「なにか必要性や面白いから定義がある」ような授業にしたい。授業づくりに協力してくれる場・学校で、新時代の授業づくりができる支援をしたい想いがある。授業を構成する教師にとって、上記の４つの分析枠組みや３つの認識様式をどのように活かすことができるのだろうか。それを現場の先生はどのようにトレーニングし実践するのか。研究・学問の範疇だけではなく、学校現場の先生につなげていきたい。
「もう気づけば３年目です」と言いながらも、これまで公立小学校と協働的に研究をすすめてきた。2018年10月～12月には、「教室を就学的にするものはなにか」というテーマで分析を枠組みをつくり、実際の使用を試みた。続いて、2019年１月～２月には、カリキュラム開発に従事している。この際も、現成主義に立ちながら、新しいカリキュラム観を構築していきたい。
今後も継続的に理論研究を進めるとともに、他教科への波及、学校現場での探索・開発と、計画は数多だ。自らの知らないものとの対話から、新しい知識を創造する・創成することに重きを置く研究の立場であれば、国内・国外問わず人間としての対話・コミュニケーションを欠かさずにしていく。（例えば、橋カレンダープロジェクトでは、生まれ故郷である呉市との交流、海外の研究者との交流を進めている。詳細は下のバナーをクリックしてください。）
解説しながら書き足す影山先生
いろんな世界と関連をして、その世界の中を動いたり、戻ったり。その中核、発信元になるEVRIにしていきたい。
知識創生研究クラスタと関連して、上述した以外にも様々なセミナーやフォーラム、活動が実施された。
